Calcul de la force de flexion lors du pliage libre d'une machine à cintrer les tôles

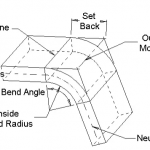
Ces dernières années, les cintreuses de freins métalliques ont été largement utilisées dans diverses industries et la gamme de traitement des cintreuses s'est élargie. Cependant, il n'y a pas eu de discussion systématique sur le calcul de la force de flexion. À l'heure actuelle, il existe à peu près deux types de formules de calcul de la force de flexion recommandées dans les manuels de divers fabricants de plieuses de presses plieuses.

P - force de flexion, KN;

S - épaisseur de feuille, mm;

l - la longueur de flexion de la feuille, m;

V - la largeur de l'ouverture inférieure de la matrice, mm;

σb - Résistance à la traction du matériau, MPa.

Le tableau des paramètres de force de flexion recommandé par le fabricant est également calculé selon la formule ci-dessus.

Le processus de dérivation et le champ d'application de la formule de calcul de la force de flexion

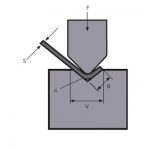
La figure 1 est un diagramme schématique du travail pendant le pliage de tôle. Ce qui suit décrit le processus de dérivation de la formule de calcul de la force de flexion et deux conditions de paramètres supplémentaires. Tout d'abord, il existe de telles recommandations dans le manuel du produit. En flexion libre, la largeur d'ouverture de matrice inférieure V choisie est de 8 à 10 fois l'épaisseur de tôle S. Ici, nous prenons le rapport d'aspect .

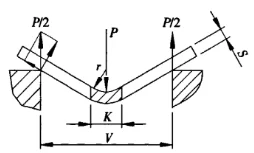
Figure 1 Schéma de principe de la flexion

P - force de flexion

S - épaisseur de tôle

V - largeur d'ouverture de la matrice inférieure

r - le rayon intérieur lorsque la feuille est pliée

K - la largeur de la projection horizontale de la zone de déformation en flexion=9

Deuxièmement, le fabricant répertorie les valeurs correspondantes de la largeur de matrice V et du diamètre intérieur r de la pièce de flexion sur le tableau des paramètres de force de flexion. Généralement r=(0,16~0,17)V. Ici, le rapport diamètre/largeur =0.16.

Pendant le processus de pliage de la tôle, le matériau dans la zone de déformation est dans un état de déformation hautement plastique et il est plié à un angle autour de la ligne médiane. Sur la surface externe de la zone de flexion, des microfissures peuvent apparaître dans certains cas. Sur la section transversale de la zone de déformation, sauf au voisinage de la couche centrale, les contraintes en d'autres points sont proches de la résistance à la traction du matériau. La partie supérieure de la couche neutre est comprimée et la partie inférieure est tendue. La figure 2 montre une coupe transversale et le diagramme des contraintes correspondantes dans la zone de déformation.

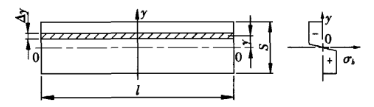
Figure 2 Diagramme des contraintes

S - épaisseur de tôle

l - longueur de pliage de tôle

Le moment de flexion sur la section transversale de la zone de déformation est :

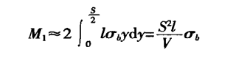
Le moment de flexion généré par l'effort de flexion de la machine dans la zone de déformation est (voir Figure 1) :

À partir de

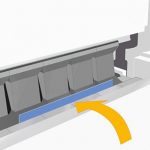
Lors de l'utilisation de moules à usage général pour le cintrage libre sur une cintreuse, la majeure partie de la tôle est pliée à 90°. Comme le montre la figure 3. K est :

En remplaçant K dans l'équation (1), on obtient :

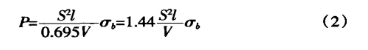
La résistance à la traction des matériaux ordinaires σb=450N/mm2, en remplaçant la formule (2) par :

On peut voir à partir du processus de dérivation que lors de l'utilisation de l'équation (2) ou de l'équation (3) pour calculer la force de flexion, les deux

les conditions paramétriques mentionnées ci-dessus doivent être remplies. C'est-à-dire le rapport d'aspect=9, le rapport diamètre/largeur=0.16, sinon cela provoquera une grosse erreur.

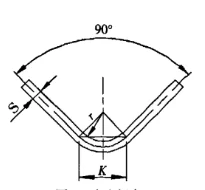
Figure 3 Flexion libre

S - épaisseur de tôle

r - le rayon intérieur lorsque la feuille est pliée

K - la largeur de la projection horizontale de la zone de déformation en flexion

Nouvelles méthodes et étapes de calcul de la force de flexion

En raison des exigences de conception ou de processus, il est parfois difficile de répondre aux deux exigences supplémentaires ci-dessus en même temps. À ce stade, la formule de calcul recommandée ne doit pas être utilisée pour calculer la force de flexion mais doit être effectuée selon les étapes suivantes.

(1) En fonction de l'épaisseur de plaque S, du rayon de courbure r et de l'ouverture de matrice inférieure V, le rapport largeur sur épaisseur et le rapport diamètre sur largeur sont respectivement calculés.

(2) Calculer la largeur de projection de la zone de déformation en fonction de la déformation de la tôle.

(3) Appliquer la formule (1) pour calculer la force de flexion.

Dans le processus de calcul, la différence du rayon de courbure et le changement de la zone de déformation correspondante ont été pris en compte. La force de flexion calculée à partir de cela est plus précise et fiable que le résultat calculé par la formule généralement recommandée. Donnez maintenant un exemple pour illustrer, comme le montre la figure 4.

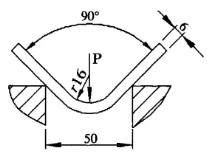
Figure 4 Nouvelle méthode de calcul

Connu : L'épaisseur de tôle S=6mm, la longueur de tôle l=4m, le rayon de courbure r=16mm, la largeur d'ouverture de matrice inférieure V=50mm et la résistance à la traction du matériau σb=450N/mm2. Trouvez la force de flexion requise pour une flexion libre.

Tout d'abord, trouvez le rapport hauteur/largeur et le rapport diamètre/largeur :

Dans un deuxième temps, calculez la largeur de projection de la zone de déformation :

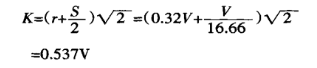
Enfin, utilisez l'équation (1) pour trouver la force de flexion :

Si la formule habituelle recommandée est utilisée pour calculer la force de flexion :

À partir de = 1,5, on peut voir que la différence entre les deux est de 1,5 fois. La raison de cette erreur est que le rayon de courbure dans cet exemple est relativement grand et que la zone de déformation correspondante est augmentée, de sorte qu'une force de courbure plus importante est requise pendant la courbure. Dans cet exemple, le rapport diamètre sur largeur = 0,32, ce qui a dépassé les conditions supplémentaires des paramètres introduits ci-dessus. Il est évidemment inapproprié d'utiliser la formule habituellement recommandée pour calculer l'effort de flexion. Vous pouvez voir les avantages de la nouvelle méthode de calcul à partir de cet exemple.

Conclusion

Les étapes et les formules de calcul de la force de flexion introduites ici ne s'appliquent pas seulement au pliage d'angle de la tôle, mais également au pliage en arc (à proprement parler, il convient de l'appeler le pliage d'angle avec un rayon de courbure extra-large). Il convient de souligner que la forme du moule est particulière lorsque la feuille est pliée en forme d'arc. Lors du calcul de la projection de la zone de déformation, celle-ci doit être calculée en fonction des paramètres technologiques définis dans le processus technologique, qui ne peuvent pas être exprimés par une formule simple.

Lors de la conception d'un moule en forme d'arc, en utilisant la méthode présentée dans cet article pour calculer la force de flexion, des résultats satisfaisants peuvent être obtenus.